

Large language models (LLMs) have exhibited great potential in mathematical reasoning. However, there remains a performance gap in this area between existing open-source models and closed-source models such as GPT-4. In this paper, we introduce MathGenie, a novel method for generating diverse and reliable math problems from a small-scale problem-solution dataset (denoted as seed data). We augment the ground-truth solutions of our seed data and train a back-translation model to translate the augmented solutions back into new questions. Subsequently, we generate code-integrated solutions for the new questions. To ensure the correctness of the code-integrated solutions, we employ rationale-based strategy for solution verification. Various pretrained models, ranging from 7B to 70B, are trained on the newly curated data to test the effectiveness of the proposed augmentation technique, resulting in a family of models known as MathGenieLM. These models consistently outperform previous open-source models across five representative mathematical reasoning datasets, achieving state-of-the-art performance. In particular, MathGenieLM-InternLM2 achieves an accuracy of 87.7% on GSM8K and 55.7% on MATH, securing the best overall score among open-source language models.
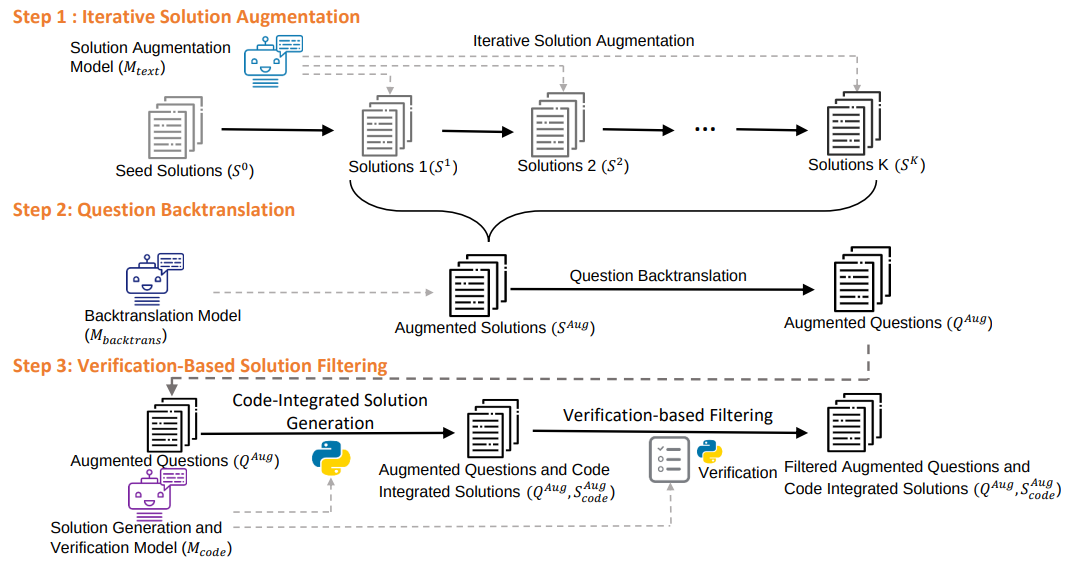
Framework of MathGenie. Iterative Solution Augmentation augments human-annotated solutions in GSM8K and MATH to create new solutions, as shown in Step 1. These solutions are then back-translated to new questions using Question Back-translation, demonstrated in Step 2. Then reliable code-integrated solutions are curated using Verification-Based Solution Filtering, by generating solutions and filtering them using verification rationales, as shown in Step 3.
Iterative Solution Augmentation and Question Back-translation aims to generate diverse and reliable math problems. The proposed math problem back-translation leverages the constraints and logical relationships inherent in mathematical solutions to create a diverse and high-quality set of new math problems. Specifically, we iteratively augment the human-annotated solutions from the relatively small training sets of MATH and GSM8K, generating a large-scale collection of augmented new solutions. These solutions are then processed by a math back-translation model to back-translate the augmented solutions into their corresponding math questions.
These newly generated math problems lack reliable ground-truth solutions, which necessitates the proposed Verification-Based Solution Filtering. We first build a model capable of generating code-integrated solutions and verifying these solutions. Then, code-integrated solutions of the new questions are generated with this model. To enhance the reliability of these code-integrated solutions, we use the model to verify the model-generated solutions by generating verification rationales for them. The verification rationales use interleaved natural language and code to verify the correctness of the solutions. Only the solutions verified to be correct are retained, thus improving the accuracy and quality of the generated data.
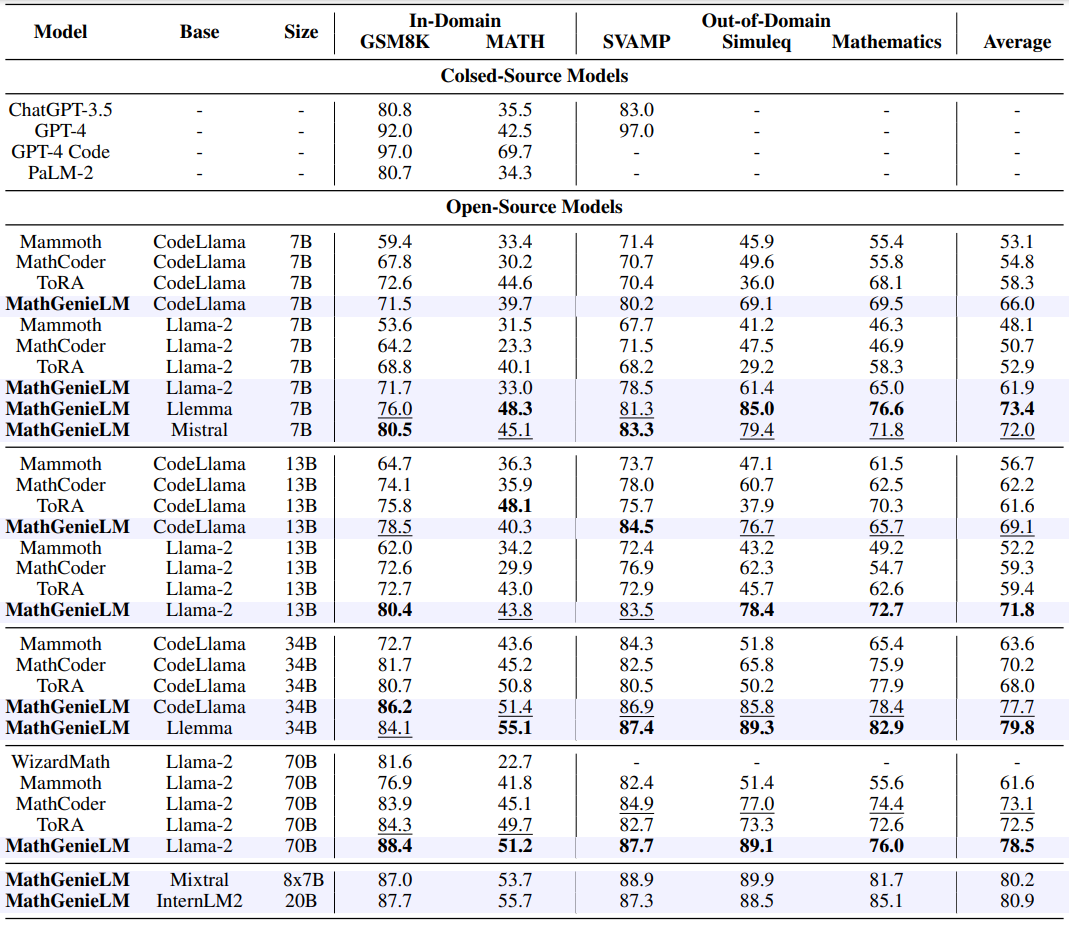
Results of MathGenieLM, compared to various open-source and closed-source models on 2 in-domain datasets (GSM8K, MATH), and 3 out-of-domain datasets (SVAMP, Simuleq, Mathematics).
Based on the results, we make the following observations: